Le principe d’Enigma
Le principe de base des machines Enigma conçues par Scherbius repose sur l’utilisation de rotors qui transforment l’alphabet clair (noté en minuscules et en vert) en alphabet codé (en majuscules et en mauve). Pour mieux l’illustrer, nous nous limiterons à un alphabet de six lettres*. Voici la représentation de l’un de ces fameux rotors, ainsi que le schéma équivalent qui permet de mieux suivre l’opération « avec les doigts ».
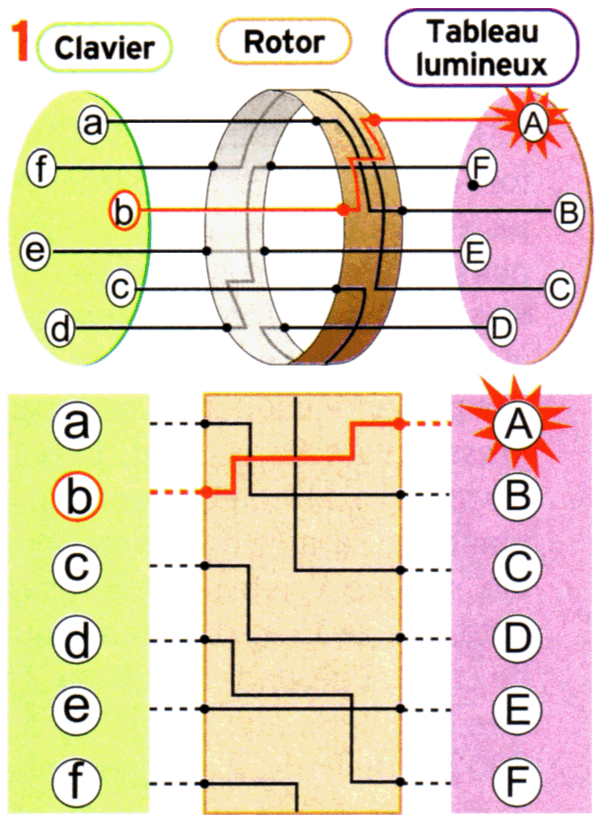
Schéma 1
Si l’on frappe la lettre b sur le clavier, un courant électrique est envoyé dans le rotor, suit le câblage interne, puis ressort à droite pour allumer la lettre A sur le tableau lumineux. b est donc codé en A. Idem pour les cinq autres lettres :
a → B, b → A, c → D, d → F, e → E et f → C.
Autre principe de base: chaque fois qu’une lettre est tapée sur le clavier, le rotor tourne d’un cran. Ainsi, b → A la première fois, mais b → C la deuxième (voir Schéma 2), puis b → E, etc.
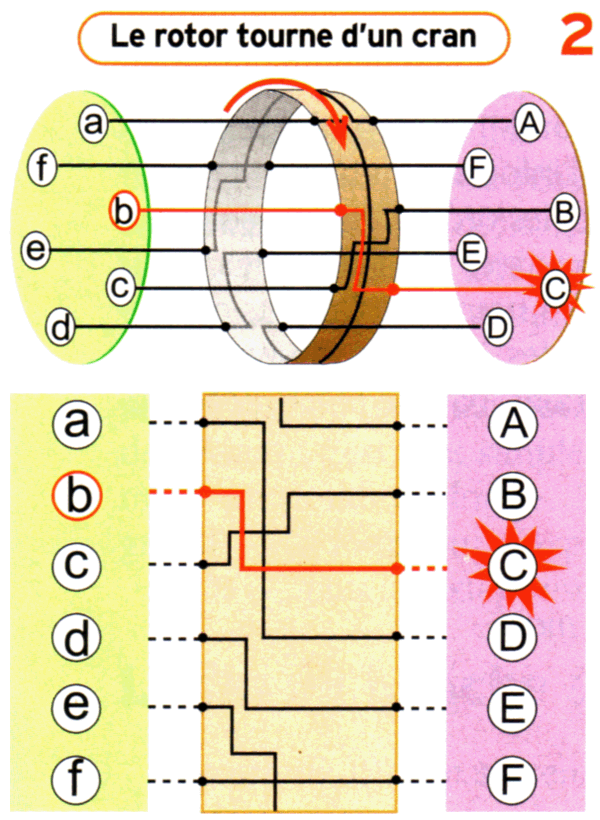
Schéma 2
Dans notre exemple, le mot bac est donc codé ADD, et non ABD si le rotor était resté immobile.
Pour augmenter le nombre de combinaisons possibles — et déjouer les tentatives des cryptanalystes —, Scherbius a associé plusieurs dispositifs, comme dans le Schéma 3.
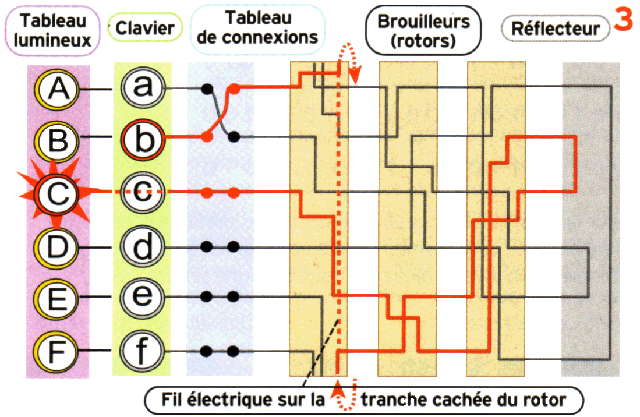
Schéma 3
Le tableau de connexions permet de brouiller davantage les pistes en reliant deux lettres du clavier entre elles (ici a et b). Ainsi, quand on tape b, le courant prend en fait le circuit prévu pour a.
Les trois brouilleurs associés multiplient aussi le nombre de combinaisons. Le deuxième et le troisième avancent respectivement d’un cran quand le premier et le deuxième ont fait un tour complet.
Quant au réflecteur, il renvoie le courant dans le dispositif jusqu’au tableau lumineux où la lettre cryptée s’affiche. Son rôle n’est pas d’augmenter le nombre de combinaisons possibles, mais de faciliter considérablement la tâche du destinataire. En effet, si b → C dans notre exemple (en rouge), on a aussi c → B. Et c’est valable pour toutes les paires de lettres claire/cryptée. Conséquence: si le mot efface est codé ACBFEB par l’émetteur, il suffira à l’opérateur qui reçoit le message crypté de taper acbfeb sur son clavier pour voir les lettres E, F, F, A, C et E s’allumer. Seule condition : les deux opérateurs distants doivent avoir réglé leurs machines Enigma de la même façon.
Au final, si l’on revient aux véritables machines Enigma équipées pour 26 lettres, on a :
- 26 x 26 x 26 = 17 576 combinaisons possibles liées à l’orientation de chacun des trois brouilleurs.
- 6 combinaisons possibles liées à l’ordre dans lequel sont disposés les brouilleurs.
- 100 391 791 500 branchements possibles quand on relie les six paires de lettres dans le tableau de connexions.
Les machines Enigma permettent donc de coder un texte selon 17 576 x 6 x 100 391 791 500 = 10 000 000 000 000 000 combinaisons différentes !
* C’est le choix qu’a fait Simon Sinqh dans son excellente Histoire des codes secrets, publiée chez JC Lattés (voir critique dans la première partie du dossier). Les schémas présentés ici en sont aussi inspirés.
Tags: Adi Shamir, Alan Turing, Arthur Conan Doyle, Arthur Scherbius, Arthur Zimmermann, Bletchley Park, Charles Babbage, Clef de chiffrement, Code ADFGVX, Code binaire, Codes secrets, cryptanalyse, Cryptographie, Cryptographie asymétrique, cryptologie, cryptologue, Edgar Allan Poe, Enigma, George Painvin, Leonard Adleman, Marian Rejewski, Martin Hellman, PGP, Philip R. Zimmermann, Première Guerre mondiale, Ralph Merkle, Ronald Rivest, RSA, Seconde Guerre mondiale, Sherlock Holmes, Substitution, Transposition, Whitfield Diffie