Naissance de la cryptologie moderne

Depuis l’apparition des premiers réseaux d’ordinateurs (reliés par des câbles spéciaux ou des lignes téléphoniques), puis l’explosion d’Internet, gouvernements, armées, banques, chercheurs, industriels, entreprises commerciales, etc., ont de plus en plus recours à la cryptologie pour protéger leurs communications. Comme toujours, il s’agit de brouiller/débrouiller les messages grâce à une technique commune de (dé)cryptage, renforcée par une clef tenue secrète. Mais en pratique, la clef n’est plus un mot, une phrase ou un quelconque document : c’est tout simplement un nombre binaire. Et plus il est grand — la longueur s’exprime en bits — plus le codage est sécurisé.

À partir de 1976, par exemple, les Américains imposèrent une technique standard de chiffrement des données (DES) reposant sur une clef de 56 bits, ce qui n’autorise pas moins de 2⁵⁶ = 100 000 000 000 000 000 combinaisons possibles ! La méthode de chiffrement consiste à brasser les bits jusqu’à plus soif : découpage en plusieurs blocs binaires de même longueur, puis moulinage avec la clef, redécoupage, remoulinage, et ainsi de suite. Pour quiconque détient la clef, l’opération de décryptage est quasiment instantanée. Pour les malveillants, en revanche, c’est une véritable galère puisqu’il faut tester toutes les combinaisons possibles. Cela se résume alors à une affaire de puissance : selon la rapidité de l’ordinateur, cette tâche peut prendre des jours, des années, voire théoriquement des millénaires !

Jusqu’en 1975, et malgré la montée en puissance des ordinateurs, les fondements de la cryptologie n’avaient toujours pas connu de véritable révolution. Pour tout dire, le vibrant « Arghhh! » poussé au XIX^e s. n’avait pas fini de résonner puisqu’aucun concept inédit n’avait été inventé. Mais deux puissants vents novateurs soufflèrent soudain sur la planète Crypta.

Ralph Merkle, Martin Hellman et Whitfield Diffie, les pionniers de la cryptographie asymétrique

La fin du bouche à oreille

Le premier ouragan balaya d’un coup le problème de la distribution des clefs. Jusqu’alors, la seule méthode véritablement sûre consistait à transmettre la clef de la main à la main, ou de bouche à oreille. Tout autre mode de transmission (messager, courrier, radio, téléphone, etc.) créait le risque que la clef soit interceptée. Cet inconvénient s’accentua encore avec l’explosion d’Internet : comment sécuriser ses messages quand le correspondant est à l’autre bout de la planète ? Pas question de faire à chaque fois le voyage pour communiquer sa clef de déchiffrement !

La solution fut donc découverte en 1975 par un groupe de francs-tireurs de l’informatique : Diffie, Hellman et Merkle. Le principe ? Il repose sur l’utilisation des fonctions « à sens unique ». Auparavant, nous avons vu que toutes les techniques de cryptage étaient réversibles : on avait beau tripatouiller les lettres d’un message ou les chiffres d’un code binaire, il suffisait de faire l’opération inverse pour obtenir le texte clair d’origine. Une fonction à sens unique, en revanche, se distingue par le fait qu’elle est très facile à mettre en œuvre, mais excessivement difficile à inverser. Ce qu’illustre à merveille l’analogie des pots de peinture (voir « Échange de pots de peinture » ci-dessous). C’est Hellman qui découvrit le premier une fonction mathématique à sens unique utilisable (fort complexe !), ce qui marqua la naissance de la « cryptographie asymétrique ».

Échange de pots de peinture

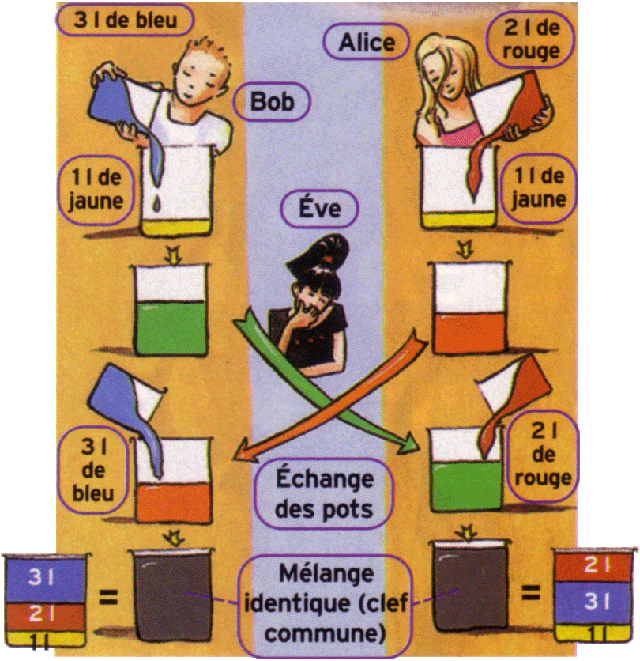
Le mélange de deux pots de peinture différents s’apparente à une « fonction à sens unique » : mélangez certaines quantités de bleu et de jaune, et vous obtenez une certaine teinte de vert. En revanche, il est impossible de retrouver les couleurs d’origine et leur quantité si vous êtes face au seul pot de vert !

Supposons que les codes binaires soient remplacés par des pots de peinture. Si Alice veut transmettre un message codé à Bob, elle doit au préalable choisir avec lui une clef secrète. Alice et Bob vont d’abord s’entendre pour utiliser un litre de couleur jaune (l’indiscrète Eve peut être au courant, ça ne change rien).

Chacun de son côté, Alice et Bob mélangent au jaune une certaine couleur qu’ils tiennent secrète. Disons bleu pour Bob et rouge pour Alice. Puis ils s’échangent les pots par un moyen quelconque : même si Ève prélève des échantillons, elle est bien incapable de déterminer les proportions exactes des mélanges !

Une fois qu’ils ont reçu le pot de l’autre, Alice et Bob y rajoutent enfin les mêmes quantités de couleur bleu et rouge qu’auparavant. Au final, et sans connaître la couleur utilisée par l’autre, ils obtiennent donc exactement le même mélange qui constituera leur clef commune. Quant à Ève, il ne lui reste plus… qu’à broyer du noir.

Pages : 1 2 3 4 5 6 7 8 9

Tags: Adi Shamir, Alan Turing, Arthur Conan Doyle, Arthur Scherbius, Arthur Zimmermann, Bletchley Park, Charles Babbage, Clef de chiffrement, Code ADFGVX, Code binaire, Codes secrets, cryptanalyse, Cryptographie, Cryptographie asymétrique, cryptologie, cryptologue, Edgar Allan Poe, Enigma, George Painvin, Leonard Adleman, Marian Rejewski, Martin Hellman, PGP, Philip R. Zimmermann, Première Guerre mondiale, Ralph Merkle, Ronald Rivest, RSA, Seconde Guerre mondiale, Sherlock Holmes, Substitution, Transposition, Whitfield Diffie